Antes de empezar, aquí tiene un libro indispensable para el aficionado/ingeniero que se interese en estos temas:
http://rapidshare.com/files/321747096/Aerodinamica_del_automovil_de_competicion.rar.htmlEste tocho de debajo trata sobre la resistencia al aire, no del downforce ( o carga aerodinámica negativa ), eso lo explica muy bien el libro que aconsejo arriba.
------------------------------------------------
------------------------------------------------
Cualquier elemento tiene una resistencia al movimiento (salvo en el espacio exterior). Si la fuerza aplicada es superior a esa resistencia al movimiento, el elemento en cuestión acelerará. Si es igual a la resistencia, pueden pasar dos cosas, que esté parado y entonces seguirá parado, o que esté en movimiento, y entonces mantendrá la velocidad. Si la fuerza aplicada es menor a la de resistencia, el elemento mecánico decelerará.
En un coche, tenemos por un lado una fuerza aplicadora, que es la del motor y que se transmite a las ruedas debidamente transformada.
Por otro lado tenemos lo que se llaman "resitencias pasivas", fuerzas resistentes que se oponen a la fuerza de la rueda. Como son rozamientos internos, fuerza de rodadura y fuerza aerodinámica.
Los rozamientos internos existen siempre que hay dos piezas en movimiento relativo, con lo cual podremos actuar sobre ellos de forma limitada a través de la lubricación y una correcta fabricación.
La fuerza de rodadura, es la que tiende a frenar la rueda por el hecho de pisar el suelo y rodar. Suele calcularse como una fraccion k del peso del coche. Fr=k . m . g, donde k es el coeficiente de rodadura (entre 0.011 y 0.014), m es la masa del vehiculo y g es la aceleracion de la gravedad (9.8 m/s2).
El coeficiente de rodadura depende a su vez de las superficies en contacto, tipo de goma de la rueda, y tipo de asfalto, además de factores que dependen del tamaño de la huella.
Y por fin vamos con la tercera fuerza en discordia, la aerodinámica.
Se define aquí como la fueza que necesita el coche para penetrar en un fluido, en este caso aire. Como veremos depende de la velocidad.
Antes de definir completamente la fuerza aerodinamica, hablaremos un poquito de los principios básicos.
Un determinado cuerpo presenta una resistencia al paso de un fluido. Esta fuerza depende del área que se enfrenta a la corriente, esto es obvio, cuando en un dia ventoso abrimos un paraguas, la fuerza que hace el paraguas sobre el brazo es muy superior a la que haría si estuviese cerrado.
Pues bien, la resitencia como digo depende del área, pero no solamente del area, sino tambien de la forma. Con esto quiero decir que para dos cuerpos que presenten un mismo area frontal a la corriente la fuerza que el aire ejerce sobre ellos, depende además de su forma. Suponeros un posavasos de forma circular, y suponeros una pelota de tenis del mismo diametro. El area frontal a la corriente es el mismo, puesto que el radio es el mismo. No obstante, la fuerza que genera el aire no es igual en ambos, es superior en el posavasos. Esta dependencia de la forma y no solo de la dimensión nos la da el coeficiente aerodinamico (Cx). Este varía con las formas y no hay hay manera de hallarlo por formulas, salvo quizás en casos extremadamente simples, sino que es experimental, es decir, hay que medirlo en cada caso.
Por tanto, la fuerza aerodinamica al depender del area y del coeficiente de forma o Cx, es proporcional a ambas, es decir a SCx, siendo S la superficie frontal y Cx el coeficiente.
Valores típicos de area frontal son 1.8 metros cuadrados para coches pequeños, 1.9 para medios, 2 para medios - grandes y 2.1 para grandes. En todo terrenos son superiores como es obvio. Un metodo aproximado para calcularlo es multiplicar el ancho del vehiculo (retrovisores incluidos) por el alto del vehiculo y por un factor que varía entre 0.8 y 0.85.
El Cx varía entre 0.26 y 0.34 para turismos.
Veamos que más factores influyen.
Pues el primero y obvio es la velocidad. A mas velocidad mas resistencia. ¿cuanto? Pues la fuerza crece con el cuadrado de la velocidad, esto quiere decir que a 100 no hay el doble de fuerza aerodinamica que a 50, sino cuatro veces más. Esta dependencia se puede demostrar con ecuaciones de mecánica de fluidos que no vienen al caso.
Otro factor importante es la densidad del medio. Está claro que cuesta mas moverse por el agua que por el aire. Esto es porque la densidad del agua es mil veces superior a la del aire. Por tanto la densidad del aire será otro factor multiplicador que llamaremos d. Valores normales son 1,225 y por cada 500 metros de altitud, disminuye un 5% aproximadamente.
Además y procedente de la mecánica de fluidos, tema que no voy a entrar por no ser el objetivo del tema, habrá que multiplicar por 0.5 todo con lo que nos queda como fuerza aerodinamica...
0.5 . d . SCx . V(2) , donde V(2) es el cuadrado de la velocidad.
Por tanto, la resitencia total (aerodinamica + rodadura) será la suma de ambas, es decir:
(k . m . g) + 0.5 . d . SCx . V(2)
Ahora la pregunta. ¿que potencia del motor hace falta para vencer esas resistencias? Como dije al principio, para que un coche alcance una velocidad determinada, hace falta que las fuerzas generadoras sean iguales a las resistentes. En este caso, y como hay velocidad de por medio, podemos decir que la potencia del motor tendrá que ser igual a la consumida por la aerodinamica y por la rodadura.
Tenemos (física de BUP) que la potencia es la fuerza por la velocidad, y al hacer el balance hemos de tomar la potencia en rueda, que es un factor de la potencia del motor "P". Este factor suele estar entre 0.8 y 0.9 (rendimiento de la transmisión).
Para las fuerzas resitentes, bastará multiplicarlas a su vez por la velocidad para obtener unidades de potencia con las que comparar.
Con lo cual nos queda lo siguiente:
(k . m . g . v) + 0.5 . d . SCx . V(3)
Con lo cual si queremos ver la velocidad maxima que podrá alcanzar un vehiculo hemos de igualar la potencia en rueda a la consumida.
0.85 . P = (k . m . g . v) + 0.5 . d . SCx . V(3)
Como vemos, nos queda una ecuacion en V al cubo, la cual resolviendola nos da un valor aproximado teórico de la velocidad máxima a potencia máxima del motor (hecho que no siempre se da porque los desarrollos son mas largos y no permiten que el motor desarrolle la potencia necesaria para vencer la fuerza del aire o cortos, de forma que en el punto donde teoricamente se conseguiría la maxima velocidad la potencia haya caído ya un poco).
Un ultimo apunte, para que la formula sea coherente, debe estar en las unidades correctas, con lo que V debe estar en metros /segundo (1 m/s = 3,6 km/h), el area en metros cuadrados y la potencia en Watios, para pasar de Watios a caballos hay que multiplicar por 0,00136.
A modo de ejemplo, para un coche que alcance 190 km/h con Cx = 0,30, area frontal = 2 m(2) y 1200 kilos de peso, la potencia necesaria es:
(0,012 . 1200 . 9,8 . (190/3.6)) + (0.5 . 1.225 . 2 . 0,30 . (190/3,6)(3) = 83,6 CV en rueda, que tras dividir por 0.85 de rendimiento de transmision son: 98,36 CV, que es sensiblemente parecido a la potencia que dan coches que alcanzan 190 km/h (unos 100 cv).
A partir de unos 100 km/h se vuelve progresivamente más importante, exponencialmente con la velocidad. A igualdad de potencia, un coche con buena aerodinámica tiene más punta, castiga menos el motor y traga menos que otro con aerodinámica mala.
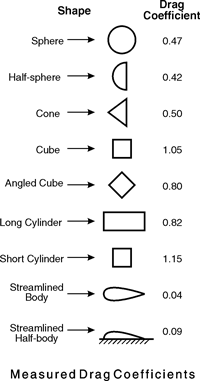
El Cx o Cd (como le dicen en automoción y aeronáutica respectively) es un coeficiente adimensional, un indicador sobre eficiencia de forma con relación a un elemento de fácil referencia (una placa cuadrada expuesta de cara al flujo a la que se atribuye arbitrariamente un Cd de 1.0). Así, una forma (por ejemplo un coche) con Cd de 0.33 tiene 3 veces mejor forma aerodinámica que la susodicha placa.
Pero el Cd, por sí solo, no nos cuenta toda la historia. Hay que conjugarlo con el área frontal del coche A (Cd·A) . Un vehículo con excelente Cd de 0.25 pero con 4 metros cuadrados de área frontal (CdA=1.0) tiene mucha más resistencia aerodinámica que tu 407. Y otro con pésimo Cd de 0.40 pero con solo 1.5 m2 de área (CdA=0.6) tendrá menos resistencia.
Cd 0.26 y CdA 0.50 el Calibra 8V (récord mundial en 1989 para coches de serie); 0.29 los demás Calibras. El truco esta en que 8V tiene ruedas de 195 y los demás de 205. Las ruedas son pésimas para la aerodinámica, cuanto más anchas, mayor resistencia.
Hoy día muchos coches tienen un Cd menor de 0.30. Más de 0.35 ya empieza a cantar y más de 0.40 no debería ser aceptable a estas alturas.
Los monovolúmenes suelen tener un Cd razonablemente decente, pero tienen más área frontal (al ser más altos) y por tanto peor aerodinámica.
Los peores del rebaño (en esto como en muchas otras cosas) son los puñeteros estorbos SUV todo-terreno, que combinan pésimos Cd con enormes áreas frontales, resultando una penosa, lamentable e ineficiente aerodinámica. Ejemplos:
- AMG Hummer: Cd 0.51 x 3.06 m2 = 1.56 (más de tres veces peor que un Calibra).
- VW Touareg: 0.41 x 2.78 = 1.14 (más del doble de malo)
- BMW X5: 0.35 x 2.70 = 0.945 (casi el doble de malo)
Un Ferrari F50 tiene Cd 0.372, un Testarossa 0.36, un F40 0.34. Son bajos y con poca área frontal, pero las enormes ruedas conspiran contra el Cd. Esto sucede en muchos superdeportivos.
Como curiosidad, los F1 suelen andar por entre 0.7 y 1.1 de Cd (según la carga aerodinámica que demande cada circuito), debido a las grandes ruedas 'al aire' y a todos los apéndices para apoyo aerodinámico. No hay problema porque con 700+ pencos lo que pierdan en punta en recta lo recuperan enhebrando las curvas a ese ritmo increíble.
Ejemplo práctico: Calibra 8V (CdA = 0.5) vs BMW X5 (CdA = 0.945), intentando ambos alcanzar 250 km/h.
Al Calibra le bastarían unos 153 CV en rueda (= unos 186 motor).
Pero el X5 necesitaría unos 286 CV en rueda (= unos 350 motor; uséase, casi el doble de pencos) para alcanzar los mismos 250 km/h.
O dicho de otra forma: Un Calibra con 190 pencos dejará atrás a un X5 aunque el zambombo tenga 350 CV.
Una hembra de la especie humana tiene un Cd de alrededor de 1.3 expuesta al flujo de pie, y 1.0 expuesta de cabeza à là Supergirl. Esto por supuesto puede variar si sus curvas son especialmente aerodinámicas y su cuerpo cumple bien la regla de las áreas.

Un par de curiosidades.
En 1921 el Dr. Edmund Rumpler (que había diseñado aviones de combate durante la guerra del 14) concibió un automóvil conocido como Rumpler Wagon. Lo hizo 'a ojo', no había túneles para coches en 1921. A la gente le hizo mucha gracia su pintoresco aspecto.

Setenta años después unos ingenieros sacaron un Rumpler del museo y lo metieron en el túnel de Lockheed en Georgia, USA, para echarse unas risas.
El ordeñador escupió '0.28' .
Desde entonces nadie se ha vuelto a cachondear del Rumpler, al contrario, se usa como paradigma de diseño eficiente.
En 1957 Sir Colin Chapman realizó el precioso Lotus Elite, primer coche del mundo con estructura monocoque en material compuesto (fibra de vidrio, lo mejor que había en aquella época anterior al carbono/kevlar/etc.).

Por aquella época la aun incipiente Lotus no tenía dineros para pagar túnel, así que de nuevo el ingeniero (Frank Costin nada menos) tuvo que dibujarlo 'a ojo'.
Muchos años después alguien metió un Elite al túnel y el ordeñador escupió: '0.29' .
Todos estos grandes hombres del pasado se revolverían despollándose en sus tumbas si nos vieran, a 2006, conduciendo zambombos todoterreno con la aerodinámica de un ladrillo.
Los caprichos de la aerodinamica:
Obsérvese como interactúa una forma no muy aerodinámica como la de un camión con remolque en movimiento con la atmósfera terrestre (el objeto se mueve hacia la derecha):
La pintoresca estela de remolinos alternativos que deja por la popa se conoce como 'callejón de vórtices de von Karmann', y significa mucha pasta perdida en consumo extra por mala aerodinámica.
La misma idea en el 'extradós' de un Mitsu Evo:

Se llaman generadores de vórtices y están inventaos hace 50+ años, pero solo recientemente algunos 'pioneros' han empezado a aplicarlos a coches de calle. Quizá no queden tan chachi pirulis como un aerofreno truñing fantasía pero son más eficientes .